MALO Lab

In the Multi-Agent Learning and Optimization (MALO) Lab, we study distributed algorithms for learning and optimization over multi-agent networks. Specifically, we design the rules for a group of autonomous agents, each having local information, to collaboratively achieve global objectives through local computation and local communication.

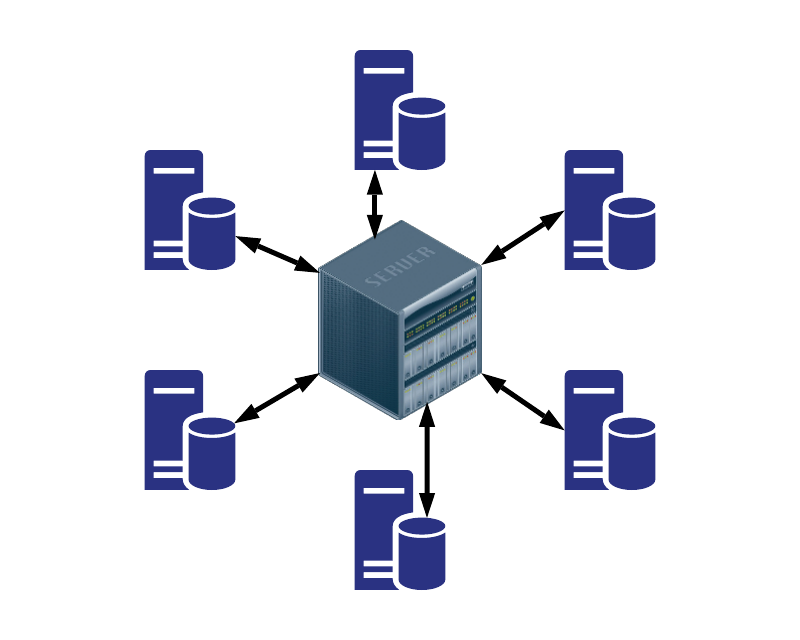
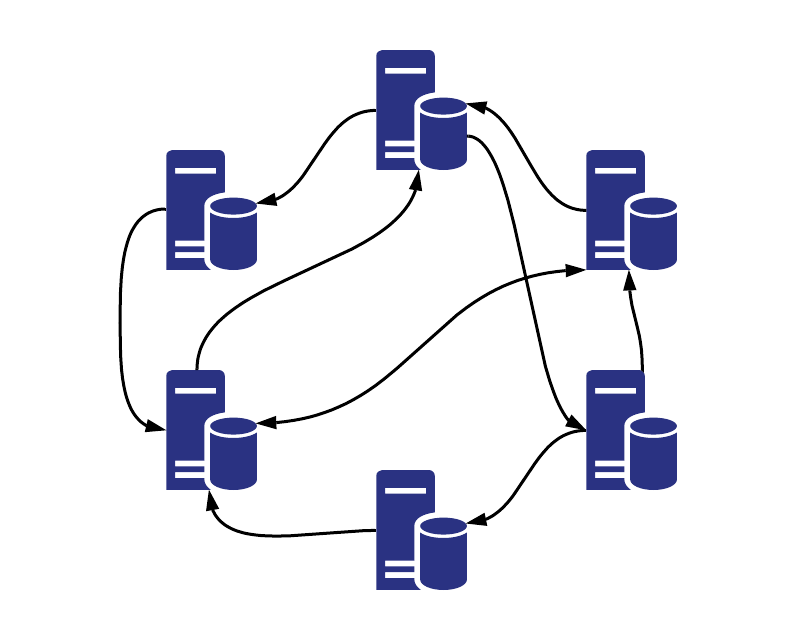
The above shows two typical computing architectures for distributed computation: centralized (left) vs decentralized (right). MALO Lab focuses on the decentralized architecture that requires no central controller and enjoys more flexibility, robustness, and lower communication overhead.

Applications of our research include large-scale distributed machine learning, resource allocation in networks, multi-robot coordination, decentralized estimation, among others.

Our research is interdisciplinary in nature and spans several areas including network science, optimization, control theory, and machine learning.

Current Projects

Distributed Optimization over General Directed Networks

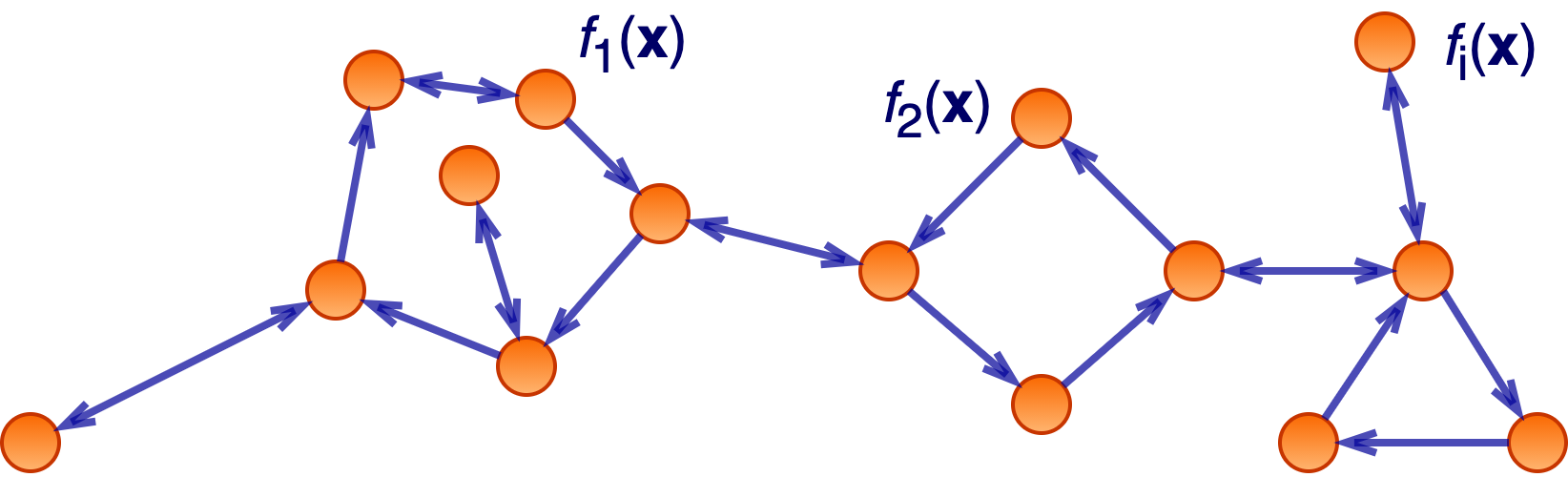
Network topology plays a central role in the design and analysis of decentralized algorithms for learning and optimization over multi-agent networks. Most existing works consider undirected networks where the information exchange is bidirectional. However, in some real-world applications, directed networks are inevitable. This project will focus on designing novel algorithms for distributed learning and optimization over general directed networks.

Related works:

• Z. Song, L. Shi, S. Pu and M. Yan, Provably Accelerated Decentralized Gradient Method Over Unbalanced Directed Graphs.
• Z. Song, L. Shi, S. Pu and M. Yan, Compressed Gradient Tracking for Decentralized Optimization over General Directed Networks.
• S. Pu, A Robust Gradient Tracking Method for Distributed Optimization over Directed Networks, 2020 IEEE 59th Conference on Decision and Control (CDC).
• S. Pu, W. Shi, J. Xu and A. Nedić. Push-Pull Gradient Methods for Distributed Optimization in Networks. IEEE Transactions on Automatic Control, 66(1):1-16, 2021. [arXiv]

Asymptotic Network Independence in Distributed Stochastic Gradient Methods

Distributed stochastic gradient methods are the workhorse for solving large-scale machine learning problems in networks. To accelerate convergence and improve the scalability of such methods, the project will focus on studying the asymptotic network independence property of distributed stochastic gradient algorithms, that is, asymptotically, distributed algorithms work as well as their centralized counterpart and is not affected by the network topology. Moreover, the project will develop algorithms with shorter transient times to achieve network independence.

See this paper for an introduction on asymptotic network independence in distributed optimization.

Related works:

• K. Huang and S. Pu, Improving the Transient Times for Distributed Stochastic Gradient Methods.
• S. Pu, A. Olshevsky and I.C. Paschalidis, A Sharp Estimate on the Transient Time of Distributed Stochastic Gradient Descent.
• S. Pu, A. Olshevsky and I.C. Paschalidis, Asymptotic Network Independence in Distributed Stochastic Optimization for Machine Learning: Examining Distributed and Centralized Stochastic Gradient Descent. IEEE Signal Processing Magazine, 37(3):114-122, 2020. [arXiv].
• S. Pu and A. Nedić. Distributed Stochastic Gradient Tracking Methods. Mathematical Programming, 187(1):409-457, 2021. [arXiv]

Communication-Efficient Decentralized Learning Methods

Existing theory in distributed multi-agent optimization mainly concerns the number of required numerical operations for reaching certain accuracy, i.e., computation complexity. However, in a distributed setting, communication costs are non-negligible and can be the key factor affecting an algorithm’s performance (especially for large-scale networks). To reduce communication costs, the project will explore communication-efficient algorithms that require minimal information exchange between agents while preserving satisfactory computation complexity. One of the efforts in this direction is incorporating communication compression techniques into the design of distributed optimization algorithms.

Related works:

• Z. Song, L. Shi, S. Pu and M. Yan, Compressed Gradient Tracking for Decentralized Optimization over General Directed Networks.
• Y. Liao, Z. Li, K. Huang and S. Pu, Compressed Gradient Tracking Methods for Decentralized Optimization with Linear Convergence.

Funding Support

We gratefully acknowledge funding support from The Chinese University of Hong Kong, Shenzhen, Shenzhen Research Institute of Big Data, Shenzhen Institute of Artificial Intelligence and Robotics for Society, and National Natural Science Foundation of China.